
Binary numbers are the fundamentals of how computer systems work. Understanding binary number systems help kids to discover the mysterious world of computers. I decided to find out the best ways to teach kids about binary numbers.
Binary numbers worksheet helps kids to learn the binary system quickly. The worksheets feature games and challenges that will stimulate kids’ interest to learn and enforce their understanding of the binary numbers system. Binary worksheets are great teaching tools for both schools and at home.
In this blog post, I want to show you what a binary system is, a few simple terms you need to know, and why kids need to understand. At the end of the blog post, you can download the free binary numbers worksheet for kids and have fun with your kids or students.
What is a binary number?
A binary number system is a base-2 number system. There are only two numbers in the system: 0 and 1. We call them the Binary Numbers.
The first number system we are normally taught is the decimal system where we count from 0 to 9. A Decimal system is a base-10 system, where we group numbers in tens. In a binary numbers system, we group numbers in 2s.
Why learn binary numbers?
In the simplest form, computers are machines that flip the binary digits on and off. There is no ambiguity for computers, it is either a YES (1) or NO (0) to them.
Computer programs are a set of instructions we give to computers. Our computer programs are then translated into machine codes – which are binary codes that a computer can understand.
In the modern computer, data is stored and transferred in a series of 0s and 1s. Yes, all your music, photos, documents on the computer are a series of 0s and 1s.
To understand how a computer and computer program works, it is essential to understand how binary numbers work. That’s why it is beneficial for new coders to have a good understanding of binary numbers.
It might sound complex to you, but it is simpler than you thought. In the remainder of this blog post, I will give you a brief introduction to binary numbers, binary conversions, and calculations.
Now we know what a binary number is, it is time to learn a few important computer terms that are related to binary numbers.
What are a Bit and Byte?
A Bit is the smallest unit of data in a computer system. It is short of binary digits. Its value could be 1 or 0. For example, there are 4 bits in binary number 1011.
Computer circuits are made of billions of transistors. A Transistor is a tiny component that switches ON and OFF by electronic signals.
In the electrical form, a BIT represents the state of ON or OFF of a transistor. A computer or machine uses series and sequences of these ONs and OFFs to process complex information.
8 bits = 1 byte
A computer is made up of billions of bits. To simplify the calculation, we group 8 bits into a new unit called Byte. A character is stored as a Byte on a computer.
For example, the character “A” can be translated into an 8-bit (1 byte) binary code 01000001.
How to count in Binary?
There are only 2 digits in the binary system: 1 or 0. To count in binary, you start at 0, then go to 1.
Just like in the decimal numbers system, where we start from 0 to 9, we go from 1 digit into 2 digits when adding 1 to 9. (1 +9 = 10).
Let’s first look at how to count in Decimal:
| 0 | Start at 0 |
| 1 | Then 1 |
| … | Keep counting 2,3,4,5,…8 |
| 9 | This is the last digit in Decimal |
| 10 | The rightmost digit back to 0, and add 1 to the left. |
Now, let’s look at counting in Binary:
| Sequence | Binary | Remark |
|---|---|---|
| 1 | 0 | Start at 0 |
| 2 | 1 | Then 1 |
| 3 | 10 | The rightmost digit back to 0 and add 1 to the left |
| 4 | 11 | Next, add 1 to the right |
| 5 | 100 | 1. Add 1 to the rightmost digit 2. The rightmost digit is back to 0 again, and add 1 to the left 2. Since there was already a 1 at the 2nd digit, it is back to 0 again 3. 1 is added to the left |
| 6 | 101 | Add 1 to the rightmost digit |
| 7 | 110 | And so on … |
Now, we have an idea of how to count in binary, let’s look at the number conversions.
How to convert Binary to Decimal and vice versa?
The binary system is a base-2 number system. Since it is base 2, there are only 2 digits: 1 and 0. To convert binary to decimal, we need to understand a simple rule:
Start from the right to left, each binary digit with the value 1 represents a power of 2.
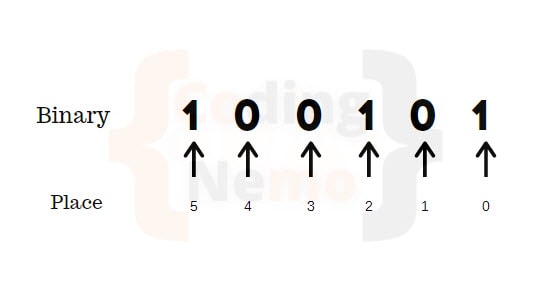
| Place (position) | 5 | 4 | 3 | 2 | 1 | 0 |
| Decimal Value | 25 | 24 | 23 | 22 | 21 | 20 |
With this understanding, it is easy for us to convert a number from binary to decimal.
Let’s use a few examples to better understand this.
How to convert a binary number 1012 and 10012 to a decimal number?
To convert a binary number to decimal, we follow the simple rules:
Start from the right to left, each binary digit with the value 1 represents a power of 2.

1012 binary = 22 + 0 + 20 = 4 +0 + 1 = 5
Let’s look at another example, binary number 10012

10012 binary = 23+ 0 + 0 + 20 = 8+0+0+1 = 9
How to convert a decimal number into a binary number?
To convert a decimal to binary, it helps if you are familiar with the powers of 2.
For example, what is the binary value of 14?
Refer to the table and steps below:
Step 1
The largest power of 2 less or equal to 14 is 23 = 8. We now know there are 4 binary digits in the answer.
So we fill position 4 of the binary with 1 (remember we start counting position from power 0)
Step 2
Next, subtract 8 from 14, we have a remainder of 6
14 – 8 = 6
The largest power of 2 less or equal to 6 is 22 = 4.
We fill position 3 of the binary with 1.
Step 3
Now, Subtract 4 from 6, we have a remainder of 2
6 – 4 = 2
The largest power of 2 less or equal 2 is 21 = 2, we fill position 2 of the binary with 1.
Step 4
Subtract 2 from 2, we have no remainder. So the calculation is complete.
2 – 2 = 0
Step 5
In the final step, we fill all empty positions with 0, in this case, position 1 is filled with 0 and we now have the binary value of 14 which is 11102.
| Binary Number | 1 | 1 | 1 | 0 |
| Power of 2 | 23 | 22 | 21 | 20 |
| Positions | Position 4 | Position 3 | Position 2 | Position 1 |
To make it a little easier for you, here is a table of power of 2s. I have also included this table in the Free Binary Worksheet Download Pack.
| Power of 2 | Calculation | Decimal Value |
|---|---|---|
| 20 | 1 | 1 |
| 21 | 2 | 2 |
| 22 | 2 x 2 | 4 |
| 23 | 2 x 2 x 2 | 8 |
| 24 | 2 x 2 x 2 x 2 | 16 |
| 25 | 2 x 2 x 2 x 2 x 2 | 32 |
| 26 | 2 x 2 x 2 x 2 x 2 x 2 | 64 |
| 27 | 2 x 2 x 2 x 2 x 2 x 2 x 2 | 128 |
| 28 | 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 | 256 |
| 29 | 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 | 512 |
| 210 | 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 | 1024 |
Here is an excellent video that explains the Binary Numbers
Free Binary Numbers Worksheets for Kids
Understanding Binary Numbers helps kids to grasp coding and computer science concepts.
I have prepared a series of worksheets. The goal is to help parents or teachers to teach kids about binary numbers. It is FREE to download.
In the download pack, you will find:
- Binary Pixel game
- Secret words game
- Answer sheet
- Binary Code Sheet
- Decode The Message play cards
- The Power of 2s worksheet
The challenge for kids is to translate the English word into binary code so that a computer can understand and decode the binary numbers, etc.
Enjoy!


